Votos de...

Geogebra

Este é um programa/software gratuito de Geometria dinâmica, construído com com o intuito de ser utilizado em sala de aula, o qual junta aritmética, álgebra, geometria e cálculo. O GeoGebra possibilita, entre outras funções, o desenho de pontos, vectores, segmentos, polígonos e funções, assim como a alteração dinâmica de cada um desses objectos.

É possível efectuar o "dowload" neste link.

Uma sequência pouco numérica...

Consideremos esta sequência de números:


2/10/12/16/17/18/19



Qual é o nº que vem a seguir?







Não, não é 20.
E para quem já pensou um pouco mais também não é 27.
Não é 21.











Já chega de andar com a cabeça às voltas, a resposta é............................................











200!!!!!!!!!!





E perguntam vocês: "Porquê?"

Esta é a sequência de números inteiros começados por "d".
Se repararem "dois" começa por "d", "dez" também, "doze" também, por aí fora.
Entre 19 e 200 não há nenhum número inteiro começado por "d".

Sítio dos miúdos

Podes ir a este endereço que te vai ligar ao site "Sítio dos miúdos", onde podes brincar e aprender Matemática ao mesmo tempo.

Intervalos de Números Reais - Aula Interactiva - 9º Ano

Curiosidade para a multiplicação

Adivinha

Esta brincadeira deve ser feita na sequência indicada. Não pules etapas, nem comeces a ler do final, senão perde a piada toda.


1- Pensa num número de 1 a 10.

2- Multiplica por 9.

3- Agora, soma os seus algarismos e subtrai 5 ao resultado.

4- Qual é a letra do alfabeto correspondente a esse número (Ex.: a→1, b→2, c→3, ...).

5- Pensa no nome de um país que comece com essa letra.

6- Pensa também no nome de um animal que comece com a quinta letra do nome do país que escolheste.






JÁ PENSASTE?


Quem foi que te disse que existem macacos na Dinamarca? Surpreso?

Problema do mês - NOVEMBRO

Lê com atenção o enunciado do problema e tenta resolvê-lo.
O João, a Inês e a Rita encomendaram uma pizza grande para o jantar. O João comeu o triplo do que comeu a Rita. A Rita comeu o dobro do que comeu a Inês. A pizza foi cortada em 36 fatias.
Quantas fatias comeram cada um dos três amigos?

Poema "Resolução de equações"

Uma equação é fogo para se resolver
é igualdade difícil e de grande porte
é necessário saber todas as regras
e ter até uma boa dose de sorte.
A primeira coisa a ter em conta
quando se olha uma equação
é ver se tem parênteses,
é que umas têm outras não.
Se tiver, é por ai que tudo deve começar.
Sinal “+” antes: fica tudo igual.
Mas tudo o que vem a seguir se deve trocar
se antes do parênteses o “-” for o sinal.
A seguir…alerta com os denominadores!
Todos têm que ter o mesmo para se poder avançar.
Os sinais negativos antes de fracções
são degraus onde podem tropeçar.
É preciso não esquecer nenhum sinal
e estar atento ao coeficiente maroto
e se um termo não interessa de um lado
muda-se o sinal e passa-se para o outro.
Quando a incógnita estiver sozinha
podemos então dar a tarefa por finda. E então,
sem nunca esquecer o que foi feito,
escreve-se o conjunto solução.

Como é que isto pode acontecer?

A Particularidade do Dígito 1

Um número composto só por algarismos 1, quando elevado a dois, proporciona um resultado, cujo número se inicia com algarismos crescentes, mas a meio do número começa a decrescer.


Ora vejamos:



111^2 = 12321

1111^2 = 1234321

11111^2 = 123454321

111111^2 = 12345654321

1111111^2 = 1234567654321

Testes Intermédios de Matemática 2009/2010

Podes consultar neste site informação sobre os testes intermédios do 3º ciclo do ensino básico.

Relembramos que as datas previstas para estas provas são:

3 de Fevereiro de 2010- 1º Teste intermédio de 9º Ano

27 de Abril de 2010 - 1º Teste intermédio de 8º Ano

11 de Maio de 2010 - 2º Teste intermédio de 9º Ano

Master Mind

Aqui está um jogo interessante e que requer raciocínio e concentração.
Boas jogadas.

Olimpíadas Portuguesas da Matemática

A Sociedade Portuguesa de Matemática (SPM) organiza, neste ano lectivo de 2009/2010, as XVIII Olimpíadas Portuguesas da Matemática (OPM).

Calendário:

1ª Eliminatória: 11 de Novembro de 2009 (na Escola Básica dos 2º e 3º Ciclos de Vale de Milhaços, Corroios)

2ª Eliminatória: 13 de Janeiro de 2010

Final Nacional: 25 a 28 de Março de 2010 na Escola Básica dos 2º e 3º Ciclos de Santa Clara, em Évora

Este concurso é dedicado a todos os alunos do 3º ciclo do Ensino Básico e Secundário. Podes obter mais informações sobre o o concurso neste site.

Se quiseres participar faz a tua inscrição junto do teu professor de Matemática.

Desafio

Desenha as seguintes figuras, sem levantar o lápis e sem repetir linhas traçadas.

M.C. Escher

O artista gráfico holandês M. C. Escher (1898 - 1972) produziu uma série de litografias e xilogravuras que procuravam representar construções impossíveis, inúmeros padrões geométricos, além de provocar no observador uma verdadeira confusão mental com suas brilhantes ilusões de óptica.

Sua obra é vasta e diversificada. Escher é geralmente lembrado como uma artista amante da matemática. No entanto, a genialidade de Escher não se limita a construir imagens com impressionantes efeitos, dotado de qualidade técnica e estética à perspectiva.

Segue-se uma apresentação com algumas das principais obras de Escher.

View more presentations from EB 2/3 de Vale de Milhaços.

Adição e subtracção de números inteiros

View more presentations from EB 2/3 de Vale de Milhaços.

Banco de itens - 2º ciclo

Se fores aluno do 2º ciclo, neste site poderás ter acesso a diversas actividades de Matemática que podes utilizar para praticar mais.

1001 Itens

Este projecto foi criado com o intuito de disponibilizar a professores e alunos do 3º ciclo um leque alargado de questões/ itens, que constituisse um recurso para levar a efeito os objectivos gerais  de aprendizagem da disciplina de Matemática. Privilegia-se aqui o raciocínio matemático, resolução de problemas e comunicação escrita.

Os itens encontram-se agrupados pelos seguintes domínios temáticos:

- Álgebra e Funções;
- Estatística e Probabilidades;
- Geometria;
- Números e Cálculo.

Matemática ao virar da esquina

Neste site podemos encontrar jogos interessantes e ligados à Matemática, tais como o Jogo do Galo, as Torres de Hanoi, Jogo do Solitários, entre outros.

Experimentem jogar, puxem pela cabeça e  pratiquem a Matemática de forma lúdica através da ginástica mental que estes jogos proporcionam.

A soma de todos os números entre 1 e 100 pode calcular-se da seguinte forma...

Conta-se do grande matemático alemão Gauss (1777-1855) que, na escola primária, o professor pediu aos alunos que calculassem a soma de todos os números entre 1 e 100, na expectativa de ficar com algum tempo livre para escrever uma carta.

Surpreendentemente, o aluno Gauss demorou apenas alguns segundos a dar a resposta, tendo descoberto o processo a seguir apresentado:

1 + 2 + 3 + ... + 98 + 99 + 100

1 + 100 = 101

1 + 2 + 3 + ... + 98 + 99 +100

2 + 99 = 101

1 + 2 + 3 + ... + 98 + 99 + 100

3 + 98 = 101

1 + 2 + 3 + ... + 50 + 51 + ... + 98 + 99 + 100

50 + 51 = 101

A soma de um par de parcelas equidistantes dos extremos é sempre 101! E quantos pares temos? 50.

Então, a soma procurada será 50 x 101 = 5050

Cartoon de Matemática

Os Números

Os números que todos usamos (1,2,3,4,5,6, etc.) são chamados “números arábicos” para os distinguirmos dos “números romanos” (I,II,III,IV,V,VI, etc.).

Os árabes popularizaram estes números, mas a sua origem remonta aos comerciantes fenícios que os usavam para contar e fazer a contabilidade comercial.

Mas alguma vez pensou por que motivo “1” significa "um", “2” significa "dois“, etc.?

Os números romanos são fáceis de compreender mas... Qual é a lógica que há por detrás dos números arábicos ou fenícios?

Muito simples:

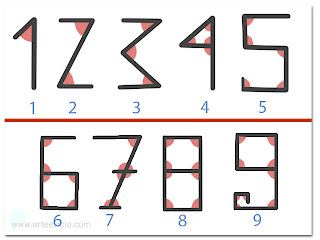
Trata-se de ângulos.

É pura lógica: Se escrever o número na sua forma primitiva, verá que:


O número 1 tem um ângulo.

O número 2 tem dois ângulos.

O número 3 tem três ângulos e assim por diante

E o "0" não tem ângulo nenhum.



E como uma imagem vale mais que mil palavras…

A Matemática anda por aí...

... PROCURA-A!