Desafio

Desenha as seguintes figuras, sem levantar o lápis e sem repetir linhas traçadas.

M.C. Escher

O artista gráfico holandês M. C. Escher (1898 - 1972) produziu uma série de litografias e xilogravuras que procuravam representar construções impossíveis, inúmeros padrões geométricos, além de provocar no observador uma verdadeira confusão mental com suas brilhantes ilusões de óptica.

Sua obra é vasta e diversificada. Escher é geralmente lembrado como uma artista amante da matemática. No entanto, a genialidade de Escher não se limita a construir imagens com impressionantes efeitos, dotado de qualidade técnica e estética à perspectiva.

Segue-se uma apresentação com algumas das principais obras de Escher.

View more presentations from EB 2/3 de Vale de Milhaços.

Adição e subtracção de números inteiros

View more presentations from EB 2/3 de Vale de Milhaços.

Banco de itens - 2º ciclo

Se fores aluno do 2º ciclo, neste site poderás ter acesso a diversas actividades de Matemática que podes utilizar para praticar mais.

1001 Itens

Este projecto foi criado com o intuito de disponibilizar a professores e alunos do 3º ciclo um leque alargado de questões/ itens, que constituisse um recurso para levar a efeito os objectivos gerais  de aprendizagem da disciplina de Matemática. Privilegia-se aqui o raciocínio matemático, resolução de problemas e comunicação escrita.

Os itens encontram-se agrupados pelos seguintes domínios temáticos:

- Álgebra e Funções;
- Estatística e Probabilidades;
- Geometria;
- Números e Cálculo.

Matemática ao virar da esquina

Neste site podemos encontrar jogos interessantes e ligados à Matemática, tais como o Jogo do Galo, as Torres de Hanoi, Jogo do Solitários, entre outros.

Experimentem jogar, puxem pela cabeça e  pratiquem a Matemática de forma lúdica através da ginástica mental que estes jogos proporcionam.

A soma de todos os números entre 1 e 100 pode calcular-se da seguinte forma...

Conta-se do grande matemático alemão Gauss (1777-1855) que, na escola primária, o professor pediu aos alunos que calculassem a soma de todos os números entre 1 e 100, na expectativa de ficar com algum tempo livre para escrever uma carta.

Surpreendentemente, o aluno Gauss demorou apenas alguns segundos a dar a resposta, tendo descoberto o processo a seguir apresentado:

1 + 2 + 3 + ... + 98 + 99 + 100

1 + 100 = 101

1 + 2 + 3 + ... + 98 + 99 +100

2 + 99 = 101

1 + 2 + 3 + ... + 98 + 99 + 100

3 + 98 = 101

1 + 2 + 3 + ... + 50 + 51 + ... + 98 + 99 + 100

50 + 51 = 101

A soma de um par de parcelas equidistantes dos extremos é sempre 101! E quantos pares temos? 50.

Então, a soma procurada será 50 x 101 = 5050

Cartoon de Matemática

Os Números

Os números que todos usamos (1,2,3,4,5,6, etc.) são chamados “números arábicos” para os distinguirmos dos “números romanos” (I,II,III,IV,V,VI, etc.).

Os árabes popularizaram estes números, mas a sua origem remonta aos comerciantes fenícios que os usavam para contar e fazer a contabilidade comercial.

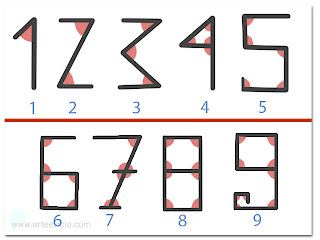
Mas alguma vez pensou por que motivo “1” significa "um", “2” significa "dois“, etc.?

Os números romanos são fáceis de compreender mas... Qual é a lógica que há por detrás dos números arábicos ou fenícios?

Muito simples:

Trata-se de ângulos.

É pura lógica: Se escrever o número na sua forma primitiva, verá que:


O número 1 tem um ângulo.

O número 2 tem dois ângulos.

O número 3 tem três ângulos e assim por diante

E o "0" não tem ângulo nenhum.



E como uma imagem vale mais que mil palavras…

A Matemática anda por aí...

... PROCURA-A!